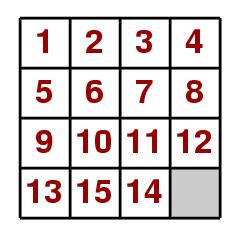
One thing I should have mentioned: I was assuming the blank space would be at the bottom right. Everything above is still correct, but the rule “even number of even cycles -> solvable” holds when the blank space is at an even position (e.g. bottom right is position 16, in your other example the blank space is at position 2).
When the blank space is in an odd position, the rule is “odd number of even cycles -> solvable”.
If I find time today I’ll put it in code…
Edit: here you go:
/**
*
* @param state A 16-length array of tiles for each position. Tile "0" is the gap.
* @return Whether this state can reach [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0] by sliding tiles.
*/
public static boolean isSolvable(int[] state){
//prepare the mapping from each tile to its position
int[] positions = new int[16];
for(int i = 0; i < state.length; i++){
positions[state[i]] = i;
}
//check whether this is an even or odd state
boolean isEvenState = positions[0] % 2 == 0;
//count the even cycles
int evenCount = 0;
boolean[] visited = new boolean[16];
for(int i = 0; i < positions.length; i++){
if(visited[i])
continue;
//a new cycle starts at i. Count its length..
int cycleLength = 0;
int nextTile = i;
while(!visited[nextTile]){
cycleLength++;
visited[nextTile] = true;
nextTile = positions[nextTile];
}
if(cycleLength % 2 == 0)
evenCount++;
}
return isEvenState == (evenCount % 2 == 0);
}
Examples:
Is the goal state solvable?
System.out.println(isSolvable(new int[]{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0}));
“true”
Is one move from the goal state solvable (having moved tile 15)?
System.out.println(isSolvable(new int[]{1,2,3,4,5,6,7,8,9,10,11,12,13,14,0,15}));
“true”
If you swap tiles 14 and 15 is it solvable?
System.out.println(isSolvable(new int[]{1,2,3,4,5,6,7,8,9,10,11,12,13,15,14,0}));
“false”
Is your other example solvable?
System.out.println(isSolvable(new int[]{1,0,3,4,6,2,11,10,5,8,7,9,14,12,15,13};));
“false”
Those are the only tests I’ve done, but the code seems to be bug free.