Hello.
Sorting has several important uses in games, but performance is usually not that important due to the data set being sorted usually only consisting of a small number of elements. However, there are cases where good performance is necessary. One of those cases is the broad phase of collision detection. The idea is simple: Sort your objects along one of the axes (say the X axis) and only process objects that overlap along this axis. In this case, sorting performance is obviously very important since the sorting part can easily get more expensive than the collision detection it’s supposed to optimize.
Sorting is difficult to do in parallel on multiple cores though. There are a few algorithms that can be partially threaded on the CPU (merge sort) and even some that can be run on GPUs (radix sort), but they generally do not scale that well with more cores. They are however much faster than single-threaded solution. Sorting for a broad phase has a very important quirk though: We can assume that the order of the objects does not change drastically between each collision detection pass due to the nature of how the objects move around. In the case of a space game with objects moving slowly through space, this is even more true.
Although O(n*log(n)) sorting algorithms like merge sort are fast for large data sets with randomly ordered elements, they’re not optimal for almost sorted data sets. A simple insertion sort is actually a very good choice in this case due to the fact that insertion sort runs at O(n) if the list is perfectly sorted already. Moving elements a small distance is also cheap, which fits my problem description perfectly. Insertion sort cannot however be easily parallelized to run on multiple cores due to the potential of a single element being moved from the end of the array to the beginning of the array, and the algorithm itself relies on that all elements before the element being processed are already sorted. However, we can make the assumption that almost all elements will only need to be moved a small distance, and we can optimize for this special case.
The idea is relatively simple. We split up the array into evenly sized chunks and use insertion sort to sort these chunks in parallel. Then we identify “overlaps” between chunks that need to be sorted to fix the ordering, and if necessary we run a second pass of insertion sorts on these overlaps. A simple algorithm is used to identify overlaps which conservatively sorts the array to guarantee correct order. The worst case is if the array is completely random, in which case the algorithm identifies the whole array as a single overlap area and the algorithm breaks down to a slow single-threaded insertion sort.
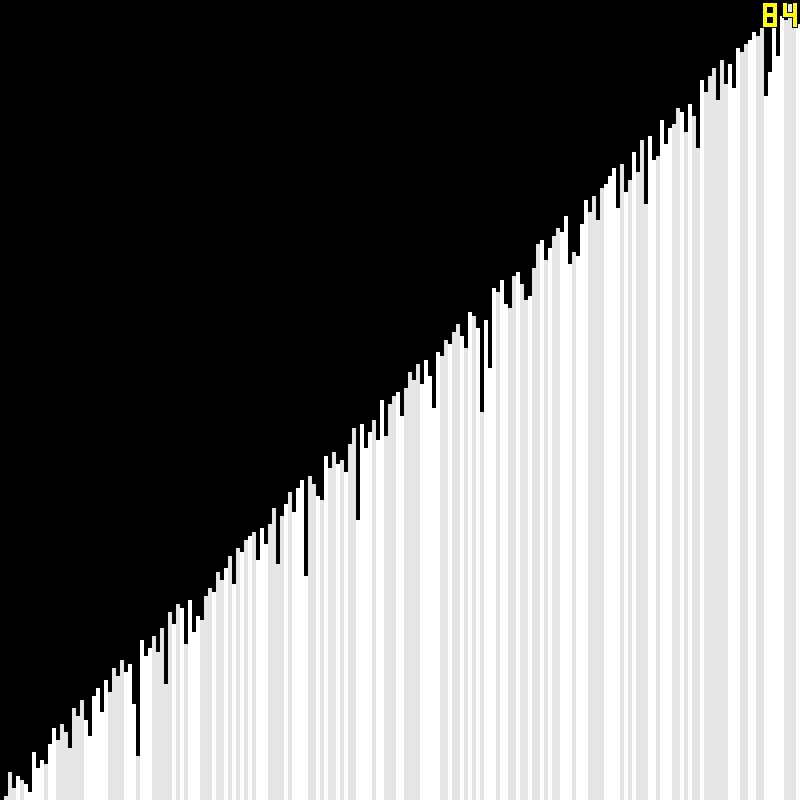
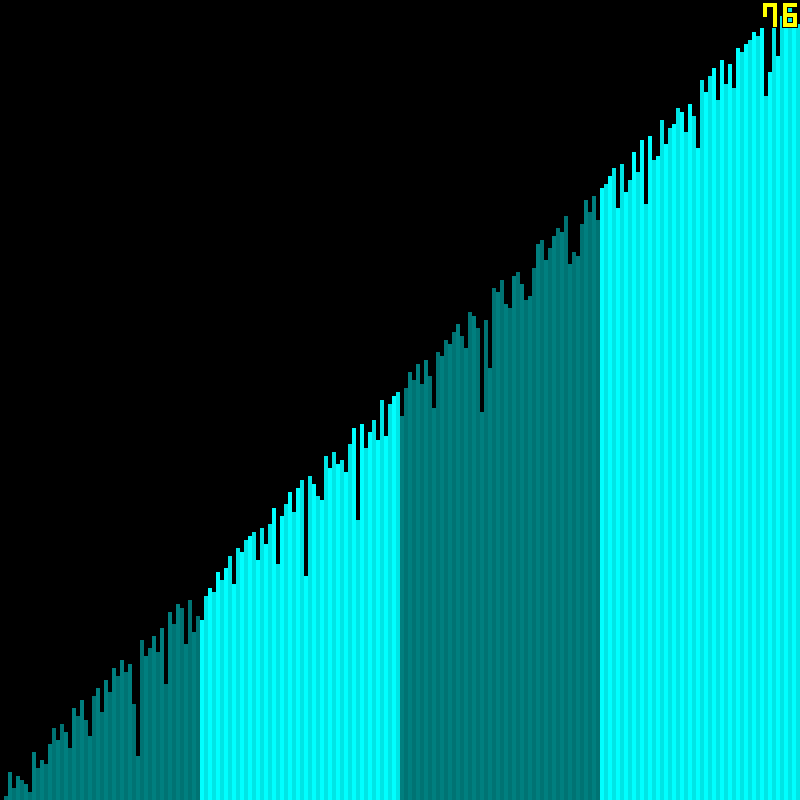
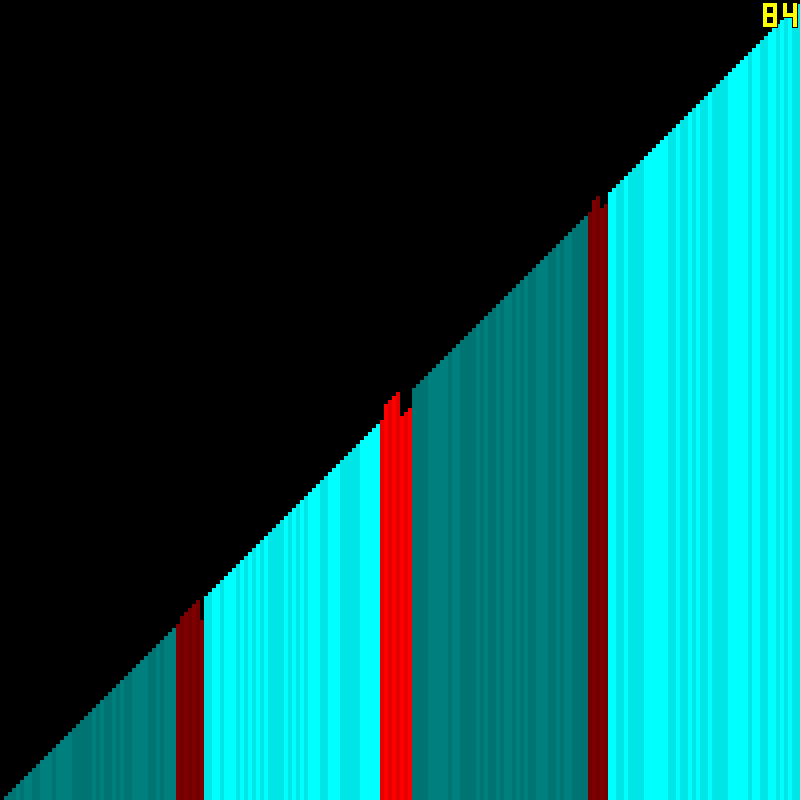
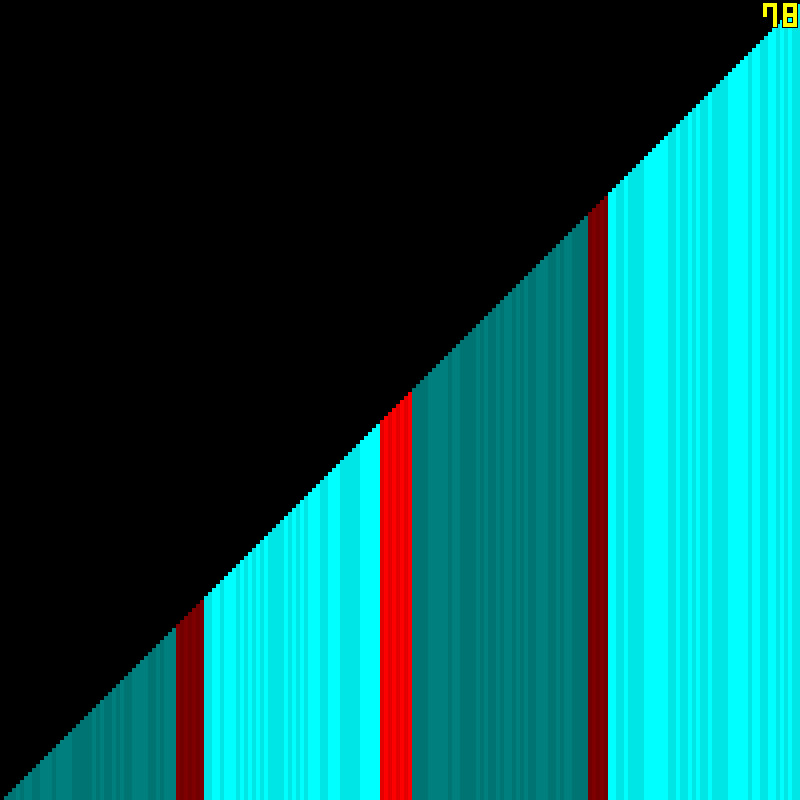
Here is a visualization of the algorithm.
To generate test data, we start with a sorted array.
We then shuffle around the data a bit to simulate the changing order of elements.
We split it up into chunks…
and sort them concurrently on multiple cores.
We identify the overlaps…
and sort them as well.
We’re done!
Performance of this algorithm is excellent. The following are the results of sorting 4 identical arrays using 4 different algorithms. The first value is for an array shuffled in the same manner as the visualization above, while the second one simply processes an already sorted list. The result is verified to be identical for all 4 algorithms (this verification is not included in the timings below). The test was run on an i7-4770K with Hyperthreading enabled. When using a single core, the processor is clocked to 3.9GHz. When using all 4 cores (8 threads for Hyperthreading) the processor drops to 3.7GHz.
Despite the lower clock speed when using all 4 cores, the parallel insertion sort achieves an almost ridiculous 6x performance boost over a single threaded insertion sort.
I also implemented the algorithm in a simple space simulation with 200 000 ships being affected by the gravity of a nearby planet. The ships first had their velocity and position updated and were then sorted by the parallel insertion sort. The below are the timings in milliseconds when using different number of cores. Both the ship updating and ship sorting is parallelized to run on any number of cores. Also note that the single core test used a non-parallel standard insertion sort to avoid the overhead of sorting the overlaps.