I am working with a mancala(kalah) game. I made the board and now want to move to the game logic.
Can anyone suggest how I should start with?
Another Question: I want to draw a hole full with ball. The number of balls can increase dynamically. How can I draw them(set Coordinate of ball), so that it seems realistic.
Thanks in advance
Mahfuz
Take a look at minmax decision trees.
It’s very easy to implement and works great in solved games (Mancala, Tic Tac Toe, and Connect 4 are all examples of solved games). Because you have enough computational resources to predict every possible game outcome from any given point, you can therefore determine at any given point what the best move is.
Here is an example of a minmax tree for Tic Tac Toe.
The game starts, no pieces are placed. The current… hmm I was going to explain this in text then just decided to Google image search if someone has made one already. 'Lo and behold.
http://www.markuslanser.com/coding/minmax.jpg
That tree obviously doesn’t illustrate every possibility because it has a lot of “…” but you should get the idea. Notice at the end they mention a “utility.” This is what you will be using to determine the proper move. As you traverse the tree and find every single possibility, you will eventually reach a bunch of leaf nodes (nodes that have no children) that all represent the end of the game (the board will be full or someone will have won). If the leaf node found is a win for the computer, then it has a value of +1. If it’s a loss, then it has a value of -1. A draw has a value of 0. Once you’ve figured out all these values for every single leaf, you’ll have your full tree created. Remember that the root node (the top) is the current game state. All of its direct children are each of your choices (see how in the image there is one for every space you can move into). You want to traverse down each of these choices to all the leaf nodes it contains, adding up the total utility as you traverse. Then the branch that has the highest utility becomes the correct choice.
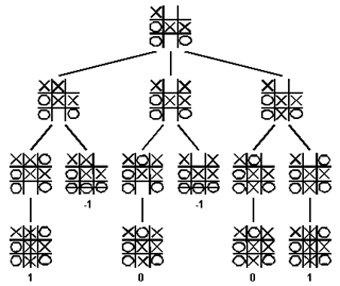
The above better illustrates that. There are only 3 choices left in the game, so there are 3 children of the root node. Every time a leaf node is reached, its utility is calculated. The total utility for the left choice is (1 + -1 = 0), the total utility for the middle choice is (-1 + 0 = -1), and the total utility for the right choice is (1 + 0 = 1). So, you would choose the right choice, which will result in the computer either winning or having a draw.
Now you just need to take that same concept to Mancala. At the start of the game, the computer will have 6 pots full of marbles and therefore 6 choices. Then you just need to branch from there, same as in Tic Tac Toe.
As for your other question, you’ll probably want to use a bit of randomness plus an angle measurement from the center, then use cosine and sine to get the X and Y.
I need to find some properties which can make good evaluation functions. So, how can make good evaluation functions?
You could try starting with just the number of secure points. That could be the number of stones already in your home bin (I don’t know the proper Mancala terms), plus one for each bin on your side with enough stones to reach your home bin.
The position evaluation doesn’t need to be perfect, it just has to help rule out really bad options.