[SOLVED] Orbital Mechanics / Velocity

Newbie & Debugging Questions
#1

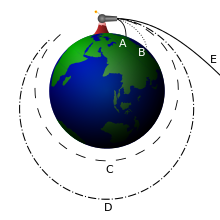
Greetings,
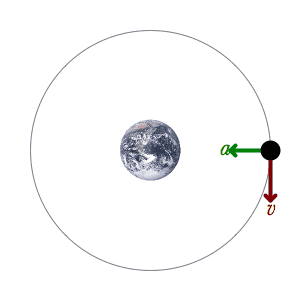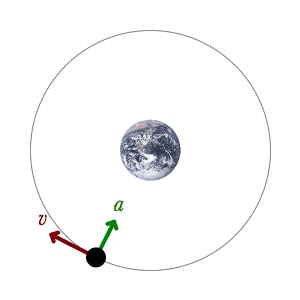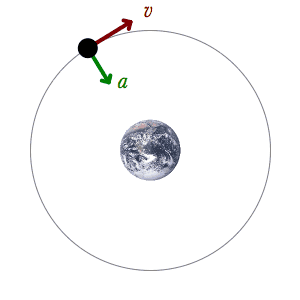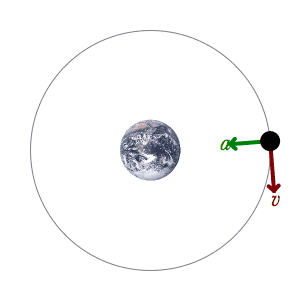
Currently working on Oribital Mechanics. The only problem I don’t know how to solve after investigating alot of time is the fact that the object in space is pulled straight down to the planet/sun… B

for (int i = 0; i < entities.size(); i++){ //go through all the planets
			if(entities.get(i) != sun){
				double distance = 0;
				for (int j = 0; j < entities.size(); j++){ //add up the gravitational effects of all the other planets
			        if (i != j){
			        	distance = Math.sqrt(Math.pow((entities.get(i).getX() - entities.get(j).getX()), 2) + Math.pow((entities.get(i).getY() - entities.get(j).getY()), 2));
				        double G = 60000;
			        	double accMag = (G*entities.get(j).getMass())/(Math.pow(distance, 2));
				        double accX = (accMag*(entities.get(j).getX() - entities.get(i).getX()))/distance;
				        double accY = (accMag*(entities.get(j).getY() - entities.get(i).getY()))/distance;
				        entities.get(i).addVX(accX);
				        entities.get(i).addVY(accY);
			        }
				}
		        entities.get(i).updatePosition();
			}
		}

This said, means that I only got the accMagnitude and I don’t know how I get the velocity. Also I know I probably should be using vectors to calculate it’s path. So my question is how I can calculate the velocity. I am probably overlooking some things right now…

As always, thank you very much
-Roseslayer

#2

V = sqrt(GM/r) , off google where V = velocity required to sustain orbit G is gravitational constant, M is the mass of the central object , and R is the radius from the center of the orbit. you can recalculate R each time . meaning say velocity is too low them recalculate when R is , then reinput R into the equation to obtain the new value.

#3

But how do I know in which direction this vector goes? Or just 90 degrees compared with the AccMagnitude?

#4

Your moon falls to the planet because you dont have any force that fights the gravity.

The moon have a speed in a direction, that is the vector Velocity.
Then you have the gravity, thats a vector from the moon to the center of the planet.

Each frame/update you calculate the gravity vector (moon center to planet center, normalized, plus gravity strength) and then add it to the velocity vector.

To start the simulation: set the position of the planet and then the position of the moon. Calculate the gravity vector and make the velocity be perpendicular to it.

Now for the moon to orbit you must find the equilibrium between moon speed and planet gravity.

If the speed is too high or the gravity too low, the moon will fly away. If the moon is too slow or the gravity too strong, the objects will collide.

UPDATE: If you dont want that simulation, forget about the Gravity and just rotate around planet. Thats the Math your using -> http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-16-shadow-mapping/

#5

+1
Is there also a calculation for the velocity in a circulair orbit?
And if I have like a moon that is orbiting a planet which is orbiting the sun, should I take both of their gravity vectors and then add the velocity vector perpendicular to it? So basically after smashing all the gravity vectors I add the velocity vector, but if I want to do that I should know a way to calculate the velocity. Any idea how I should accomplish that?

#6

For the precise speed/velocity needed I need to do some research.
Adding all the “gravitys” can do the trick.

Looking at Wikipedia -> http://en.wikipedia.org/wiki/Escape_velocity
http://es.wikipedia.org/wiki/Velocidad_de_escape

Try the speed to be sqrt(2 * g * r).
g = gravity
r = orbit radius

Let me know what you find, I’ll need it someday…

#7

The only problem for that is that I need to work with vectors, and I believe Java hasn’t a build in function for that so I need to design my own class. Having a bit of trouble with all the degrees, because if I am using tangets on a circle I will get some devided by 0 errors… Also it’s quite hard to figure out the degrees for the vectors, because of that…

#8

not sure if thats what you’re looking for … but if you want to simulate stable orbits, then maybe you already read about integration, verlet, euler, runge-kutta etc. … anyway, for stable orbits pick leapfrog :


#9

Yep, but vectors are really usefull, it is worth to code some simple vector class. Add the end, everything that you have on the screen can be calculated as a vertor, position, speeed, etc.

#10

I need to thank you all for your time, but I need to have a global picture of what I am dealing with.
The thing I want to accomplish is like a solar system with all the planets having a circular orbit (periapsis=apoapsis) and some moons having circular orbits around those planets. The only things I want to have a non ‘static’ path are comets. Could someone inventory the way how to accomplish this? like step by step a small procedure? I don’t need any codes about it, just the procedure, or rather improve my procedure

Procedure

  • Every entity has a mass, starting position and the planet it is orbiting
  • Iterating all the entities and adds it change in position. This change in position is measured by the speed and the radius if the periapsis=apoapsis the radius is also the periapsis/apoapsis. Knowing this a circle around the sun(or planet it’s orbiting) is Length = pi^2*radius. Having measured the length of the path you can get the angle by velocity/(length/360) = degrees. Having these degrees you can calculate the x and y that needs to be added.
  • Iterating comets?

Well as you still see I’ve some problems concerning comets and their calculations… If there is anyone that knows the procedure to do that? The things I know now is that you need to calculate the vector of all the gravities together and then add velocity perpendicular to it. But I need a somewhat more specified procedure to do that…

[Edit]
It is also in 2 Dimensions, forgot to say that …

#11

Kepler’s

#12

Don’t do maths. Put them on elliptical railroad tracks with elliptical paths stored in a data file - no Newtonian mechanics, integration etc needed, and you’ll need a fraction of the compute power.

#13

@ags1,
Well wow. How did I be so stupid, this will be alot easier! No algorithms mechanics needed just put them in a plain static path like the other entities. Thank you very much!

[EDIT]
Well it’s solved now. there is almost no CPU required this is all the code

this.angleMagnification = -(Math.toRadians(360/(circumference/speed)));

public void tick() {
	tick++;		
	this.x = (float) (orbiting.x + radius*Math.cos(angleMagnification*tick));
	this.y = (float) (orbiting.y + radius*Math.sin(angleMagnification*tick));
}

Thank you all very much and for your time spend. :heart:

#14

@ags1: That’s what Kepler’s gives you but the data is correct.