Hi,
I expect a very simple answer, but beyond me. I’ve done some searching but can’t find anything.
I want to rotate a sprite at a constant rate a tick so it will try to face another sprite.
I can calculate the angle between them, it’s dealing with the rotation increment/decrement when the angle crosses the 360 degrees mark to 0 degrees, messes up my code and I just can’t think through it.
Many thanks for any help!
angle = cos-1((a / |a|) dot (b / |b|))
That will give you an angle between -180 and 180. For the sake of brevity, I will assume you understand the vector math, but if not, feel free to ask. Using that number you can do something like this.
if(Math.abs(angle) < turnSpeed)
{
thing.setDirection(Math.atan(thing.x - target.x, thing.y - target.y);
}
else if(angle > 0)
{
thing.rotate(-turnSpeed);
}
else
{
thing.rotate(turnSpeed);
}
You are using two arguments in Math.atan. Might want to switch it to Math.atan2 (which is a better method by all means).
Math.atan2(y, x) is the correct function parameters, you used Math.atan which only takes 1 parameter.
Thanks for the help, I’m relatively new to Vector Maths, is this code looking somewhat right?
Written in the update method of an entity, trying to point towards the player.
Vector2 p1 = new Vector2(x/Math.abs(x),y/Math.abs(y));
Vector2 p2 = new Vector2(player.x/Math.abs(player.x),player.y/Math.abs(player.y));
float angle = (float) Math.acos(Math.toRadians(p1.dot(p2)));
There are a number of things I did not correct. It should be sin and the cross product. A is the direction of thing. B is the vector from thing to target.
I don’t think that’s exactly correct. All you need is Math.atan2 or the dot product. Where did you get sin and cross product from?
PlayerAngle = (float) Math.toDegrees(Math.atan2(player.x-x, player.y - y));
This will give me the angle between -180 and 180, I’m not sure what the need for the dot product is?
Edit:
Sorry, you said ‘or’, my bad!
Ok, so currently I am at this:
playerAngle = (float) Math.toDegrees(Math.atan2(player.x-x, player.y - y));
turnSpeed = 2;
if(Math.abs(playerAngle) < turnSpeed)
{
rotation = playerAngle;
}
else if(playerAngle > 0)
{
rotation -= turnSpeed;
}
else
{
rotation += turnSpeed;
}
At the moment it seems I am only accounting for the angle between two co-ordinates, and not the current rotation of the entity. It’s integrating that part that I’m finding most difficult.
playerAngle = (float) Math.toDegrees(Math.atan2(player.x-x, player.y - y));
This line is wrong. It should be
playerAngle = (float) Math.toDegrees(Math.atan2(player.y-y, player.x - x));
Oh yeah, cheers.
I’m still confused on how to get this fully working though. Merely using playerAngle won’t account for the entities current rotation, it’ll only give the angle between two points. The entity will just spin infinitely as playerAngle will never change so long as it is static, despite it rotating. How do I factor in it’s rotation?
Thanks
Just an offtopic question: Why the heck is it (y, x) and not the usual (x, y)?
That’s just the order the atan2 function in java’s math library wants them.
Actually it is important that you use the right inverse function to get the right sign. Intuitively, you want to put yourself in the position of your character and facing the same direction. You turn clockwise if it is to your left, counter clockwise if it is on your right, or face the target directly if is right about in front of you. Atan will give you an absolute angle. The dot product will tell you if something is in front or behind you. To make the sign tell whether you are on the left or right, rotate the direction you are facing 90 degrees and use that with your dot product. In 2D, that is like taking the Z-component of the cross product.
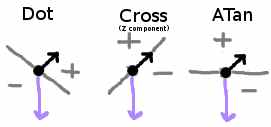
I was thinking cross product because swapping the order for two vectors changes the outcome while dot product does not. That gives you the correct sign and I think the right angle if you use sin-1. I was thinking my answer was applicable in 2D or 3D, but I will have to look at the math to figure out what my train of thought really was. In 2D, you could subtract two absolute angles from each other and adjust the answer to get the right sign.
If all the numbers work out, you could do the same thing I wrote in one line. [icode]thing.rotate(Math.max(-maxTurn, Math.min(maxTurn, angle)));[/icode]
Even if you don’t get the right sign, you can still do a few calculations to get the right one.
And I think the reasoning for y being first in the Math.atan2 function is because its sort of like slope:
sin(a) / cos(a) = tan(a)
You can use a cross product to do the rotation as well, just do:
thing.forward x (target.pos - thing.pos)
where thing.forward is the forward vector of the sprite to be rotated (which doesn’t need to be normalised).
Then as you show on your diagram, -ve or +ve Z indicate which way to rotate. Then keep rotating until the abs of the cross-product is below a threshold.
Remember if you use the dot or cross product, you should be doing it with vectors and not the positions as you are using here. So as I said above, you want to use the entity forward (direction) vector and entity->player vector.
e.g. with cross product
// Get vector from entity to player
double wx = player.x - x;
double wy = player.y - y;
// Entity forward vector
double vx = Math.cos(rotation);
double vy = Math.sin(rotation);
// Cross-product of the two vectors - sign of result signals if the
// player is in a clockwise or counter-clockwise direction
double cross = (wx * vy) - (wy * vx);
// Rotate entity towards player
if (Math.abs(cross) < turnSpeed) {
rotation = Math.atan2(wy, wx);
}
else if (cross < 0) {
rotation += turnSpeed;
}
else {
rotation -= turnSpeed;
}
Those calculations are in radians, but hope you get the gist.
Edit: Actually one other thing you need to check with the cross product is that the entity is not facing directly away from the player (i.e. 180 degrees), as the cross will also be zero then. You can do that with a dot product.
You need to normalize w.
Not if you’re only checking the sign
True, but you are also checking its magnitude on line 14.