Hi all, this is a continuation of my first tutorial: Ray Casting
In this tutorial, I will be going over the Math involved in Line-Plane intersection, and also how to implement it.
The basic idea of what is going on is very simple, first we get 3 coordinates from a plane, the convert it to a plane equation, then use the Ray from the Ray Cast to find the intersection point on the plane.
The only values you need (other than mouse coords) are 3 random points in the plane you want to intersect.
For this whole tutorial, I will use the values below:
Plane Coordinates:
A = (0, 0, -1)
B = (1, 2, -1)
C = (1, 3, -1)
Mouse Coordinates:
start = (1, 1, 1)
end = (1, 1, -2)
Ok, lets get into it. First off, I like to make a hell of a lot of floats, just to make it easier on me.
float x = 0, x1 = A.x, x2 = B.x, x3 = C.x;
float y = 0, y1 = A.y, y2 = B.y, y3 = C.y;
float z = 0, z1 = A.z, z2 = B.z, z3 = C.z;
Now, we will do some math.
Here is the matrix that we are going to mimic.
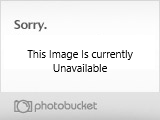
We will make 3 float arrays, x Column, y Column, and z Column and put in the values corresponding to the matrix.
float[] xC = new float[]{x - x1, x2 - x1, x3 - x1};
float[] yC = new float[]{y - y1, y2 - y1, y3 - y1};
float[] zC = new float[]{z - z1, z2 - z1, z3 - z1};
We will get the multiplication values for each row. This will be done by covering up the row we are solving for and cross multiplying the values in the other rows.
float addI = (yC[1] * zC[2]) - (yC[2] * zC[1]);
float addJ = ((xC[1] * zC[2]) - (xC[2] * zC[1]));
float addK = (xC[1] * yC[2]) - (xC[2] * yC[1]);
Sorry if the names confuse you with what they are used for.
What we will do next is find out how many of the variable T we have in the equation:
float numOfTs = (addI * (end.x - start.x)) + (addJ * (end.y - start.y)) + (addK * (end.z - start.z));
Following that is figuring out the sum of any numbers in the equation:
float num = (addI * (x1)) + (addJ * (y1)) + (addK * (z1)) - (addI * start.x) - (addJ * start.y) - (addK * start.z);
Now that we have that, we can solve for T:
float t = num / numOfTs;
Now we can essentially plug T back into the equation to find X, Y and Z
x = start.x + ((end.x - start.x) * t);
y = start.y + ((end.y - start.y) * t);
z = start.z + ((end.z - start.z) * t);
I am sorry that this is not in depth, Vector Math is very new to me and I just wanted to get a tutorial out there because I struggled to find anything myself.
Here is my final source code:
float x = 0, x1 = A.x, x2 = B.x, x3 = C.x;
float y = 0, y1 = A.y, y2 = B.y, y3 = C.y;
float z = 0, z1 = A.z, z2 = B.z, z3 = C.z;
float[] xC = new float[]{x - x1, x2 - x1, x3 - x1};
float[] yC = new float[]{y - y1, y2 - y1, y3 - y1};
float[] zC = new float[]{z - z1, z2 - z1, z3 - z1};
float addI = (yC[1] * zC[2]) - (yC[2] * zC[1]);
float addJ = ((xC[1] * zC[2]) - (xC[2] * zC[1]));
float addK = (xC[1] * yC[2]) - (xC[2] * yC[1]);
float numOfTs = (addI * (end.x - start.x)) + (addJ * (end.y - start.y)) + (addK * (end.z - start.z));
float num = (addI * (x1)) + (addJ * (y1)) + (addK * (z1)) - (addI * start.x) - (addJ * start.y) - (addK * start.z);
float t = num / numOfTs;
x = start.x + ((end.x - start.x) * t);
y = start.y + ((end.y - start.y) * t);
z = start.z + ((end.z - start.z) * t);
