Precomputed tile paths for pathfinding?

Newbie & Debugging Questions
#1

Hi,

I’m trying to solve a pathfinding problem. I’ve read that it’s possible to precompute a table of pathfinding routes based on a static map of nodes, thus making pathfinding from one particular node to another very easy at runtime.

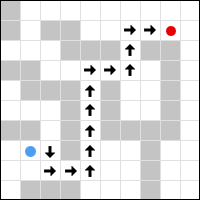
Consider this image:

In the image above, the level is comprised of a grid-based layout, with either ‘walkable’ or ‘non walkable’ tiles. Therefore, the possible range of tiles that can be walked upon are any that show as white (clear) in the diagram.

Taking the example in the image, I want to be able to select any random point on the grid - shown in the image as the red dot - and have the player walk to that location, taking the ‘best route’ possible.

I know about A*, but I’ve also read that precomputed paths is also a worthwhile direction to go in. Considering the grid size of this game is likely to only be around the 20 x 20 mark (400 tiles) would this be a worthwhile way of calculating paths? Although I sure that A* has innumerable benefits - the structure of the levels will never (ever) change, so surely a dynamic run-time solution isn’t required?

I’d apprecaite anyone’s thoughts on this.

Thanks for your time!

#2

If it’s 20x20 then forget about optimizing and just select the pathfinding you like the best (unless you are doing something really unusual with these 20x20 map like 100 units that do pathfinding per tile).

As for nodes, I never did these but it is for rather big maps. For something that small most likely it will have an opposte effect and hinder the overall performance (I think).

#3

This thread might help you:

#4

Is there anything that will ever cause a blockage, like an ‘enemy’ positioning itself on the map? If so, precomputed paths are completely worthless.

Further, you wouldn’t want to store the actual path, instead you’d want the cost from this tile to a specific goal. However, even doing that is going to be expensive. It’s going t be approximately NN, where N = XY. And that’s just for a single room.

If you’re not going to have variable cost ground movement, then you can use A* with just euclidean or Manhattan and get pretty good results.

#5

If its a very very tiny map. (your map would qualify) then you dont even need a pathfinding algoryth.

Give each walkable tile a number. (you have 65)

Then (by hand) note down for each tile in wich direction you must walk (lets say you use 4 directions)
to reach another tilenumner.

This would build a map, wich can pathfind from any position to any other position without any! pathfinding at runtime.
The Agent just need to know its current location, the target location, and then choose the direction (stores in the current tile) to walk to.

Example, you are on the blue-dot tile (tile number 23), going to red tile number (56)
You have to go west
as you store for each tile in tile number 23 where to go
like (N,S,E,W for directions)
Thus Reaching node 28, where you go south… etc.

1 N
2 N
…
10 E
11 E
12 S
…
22 W
23 W
…

Ok this sounds silly, but I actually did something like that years ago with a shooter-map having around 100 nodes.
But using some graphical method to speed this up a lot.

Technically you can let the computer precompute the path-node storage of course using A*, a flood-fill or any other pathfinding method.

10 Years ago it would have even made technical sense on slow (nokia) JavaME phones.

#6

The problem with precomputing is the insane amount of memory that is needed for it. For example, you can store a direction to every other tile in each tile for only two bits each, but this still balloons up insanely:

10x10 map: 10x10 tiles, each with a 10x10 direction map = (101010*10) * 2/8 bytes per tile = 2500 bytes. Well, that’s nothing really…
100x100 map: 100x100 tiles, each with a 100x100 direction map = 100^4 * 2/8 = 25 000 000 bytes = 23.84 MBs. Yes, that’s megabytes.
200x200 map: 200^4 * 2/8 = 381,5 MBs.

The problem is that memory usage scales with (the number of tiles)^2. Going from 100x100 to 200x200 is a 4x increase in the number of tiles. This leads to a 16x increase in memory usage. Yikes.

#7

You can reduce the growth factor of n^4 to about n^2+n, if you only store the diff with the previously calculated 2d grid. You’d do this by layering (a specialized implementation of) HashMaps.

Memory usage goes down drastically, performance hit is constant (maybe factor 10 or 100) but still fast enough.

#8

I understand how you feel about making the runtime simpler (and maybe more predictable). I’m interested in your findings, because I might do similar for the maps in my game (currently I just compute paths with A* at runtime).

Keep in mind that pre-computed paths might require a lot of data (the directional technique suggested by Damocles sounds like a fine way to store the pathing in the map, but heed theagentd’s warning). It depends on whether you need to reduce runtime CPU or RAM (if either are really a constraint).

One reason to use pre-computed paths is if you need to hand-tweak something. For instance, A* might give an optimal path, but for whatever gameplay purposes, you might want to offer a different route from some A to B. You could feasibly hand-tweak the paths if the application simply uses static data. Then again, you can also include weighted nodes in A* to make some nodes “heavier” (less desirable for pathing).

The simplest answer is probably just to implement a simple A* algorithm.

#9

O_O I have no idea what you just said, but please elaborate. What previously calculated 2D grid?

#10

You start with a generating a distance map to with (X,Y) as starting point. You process the distance-map, and turn it into a flow-map (X/N/W/S/E).
You start with a generating a distance map to with (X+1,Y) as starting point. You process the distance-map, and turn it into a flow-map (X/N/W/S/E).

Now you diff the two maps. There will (most likely) be only a fraction of all tiles that have a different value in the flow-map. The most likely places where there will be a difference, will be on the lines (X,*) and (X+1, *), and the grid (X-1…X+2, Y-1…Y+1), you can make a special case for these, as it’s probably simply swapping those lines, and moving that 3x3 sub-grid along the X axis. After that, you calculate the diff of these flow-maps that you predict will be there, for even less mismatches. I think that on average, with these additional corrections, you’re dealing with a handful of tiles with a different value.

You have your first distance-map fully stored in a Map<Coord, Direction> collection.
The second distance-map only holds the tiles that were modified.

When you lookup a distance-map for layer N, you iterate over all the entries of the diff-map of layer N. Every tile that does not have a value, can be looked up in the layer beneath it, until you reach the root, which by definition holds all tiles in the grid (as it’s a diff-map of layer 0 and Nothing).

Basically, you can compare it with a lossless video codec, with very specific knowledge of the coherence of frames.

#11

Thanks, everybody, for the insightful and helpful posts on my original question.

Given that the tile grid size example I gave could possibly be increased somewhat (maybe 50 x 50?), I’m reticent to choose a solution that could balloon memory usage - especially since there’s every possibility that the game may end up on a mobile device where memory is a pretty valuable resource.

I’ll likely follow the advice given in avoiding precomputed pathfinding for that very reason.

Regarding A-star, is there (and I hate myself for saying this) such a thing as a ‘dummies guide’. The engine itself is fully tile-based, being a roguelike game, and therefore things like distances between one position and the next will remain constant (i.e. by the tile size for lateral movement, or with the square root of the squares of the 2 tile sides for diagonal movement). I have no idea if this simplifies A*, but part of me doubts it.

I’m fairly well versed in the language, but this will be first time for delving into pathfinding - so I’m ideally looking for a resource online that can lead me gently on this topic! I’m sure someone out there knows of a very useful and easily comprehendable resource :slight_smile:

Thanks again for all your help - and any you can offer re: an A* learning resource.

#12

As coverage of the topic goes, it doesn’t get much better than http://theory.stanford.edu/~amitp/GameProgramming/

This one is also good: http://www.policyalmanac.org/games/aStarTutorial.htm

A* is indeed made easy by being on a grid, since the obvious heuristic is “Manhattan Distance”, the trivially computed number of grid squares you’d have to move if there was nothing in the way.

A roguelike with lots of rooms with exits lends itself very well to hierarchical pathfinding, which is simply where you put every location in a zone, then pathfind between zones. When you discover “waypoints” between zones, you can easily cache the paths between them. A real world example of this would be “to get from Prospect Park in Brooklyn to the Bronx Zoo, drive through Queens or Manhattan”

#13

I do have a question about what you’re intending to make. Because I can’t really think of a game that needs a pathfinder that functions on a completely static map. Maybe the walls/floor tiles won’t change, but typically there will be something like objects/entities on the map that will change how your path finder will work and which is best for you.

#14

Pathfinding on the last known static map then handling the case of running into obstacles when they’re hit or otherwise detected is pretty decent sim behavior. The actors on the map aren’t supposed to be omniscient.

#15

As mentioned before, it’s a Roguelike game; but I understand your query over the absence of dynamic entities on the map.

I was under the impression (previously) that precomputed paths worked on the basis of providing a specific (precalculated) route from any one position to another. Therefore, on the assumption that the player is moved to each of the intervening positions during the movement phase, I could check for dynamic entities ‘en route’, so to speak, and handle any potential collisions on the path.

So assuming that a path from A-G took the basic route:

A -> B -> C -> D -> E -> F -> G

The player would start moving from each point to the next. But supposing the player was at position D, and an enemy was on tile E, the player would be stopped on their travels, and have to deal with the encounter - the code preventing the rest of the path from being ‘played out’.

Then, once the enemy was defeated (hopefully!), the player would presumably attempt to continue on that path - but the path would now be something like:

E -> F -> G

My reasoning here was that I was under the assumption that a precomputed path provides information about the next node on any particular route - allowing me to ‘peek’ at that node’s location before committing to a move action, thus being able to respond to things like enemies, doors and so forth.

However, for some of the reasons explained above (memory, etc.) I’m going to try and write an implementation of A*.

Thanks to Sproingie’s links, I’m starting to get a handle on how it all works - although it does look pretty CPU intensive!

#16

[quote]it does look pretty CPU intensive!
[/quote]
Yes, pathfinding eats tons of CPU, it’s easily the biggest CPU hog in a game like Dwarf Fortress (which is why cats are such a bane, since they’re always goal-seeking toward vermin or fish bones they pick up, not to mention always getting in the way). Hierarchical pathfinding and caching can help, but you’ll still have to budget a lot of CPU for it regardless. There are GPU pathfinding algorithms out there, though none I’ve been able to find usable source for, let alone actually understand.

#17

Hmmm, could be useful to have a Player based pathfinder for rogue like, however part of the appeal of a rogue like is the control over your movement. It seems to me that instead of having the pathfinder stop on enemy collision, it should stop when a seen enemy crosses your path or something like that.

But this will really depend on how intelligent you want your pathfinder to be, and what part it’s going to play in your movement control scheme in game. If you’re implementing anything like an ‘Explored area’ service. You’d only want your A* to function on the known areas (Since you have a map of it), instead of on the unknown portions. Otherwise it leads to really allowing Pathfinder Precognition Syndrome… If you’re moving to an unexplored area, you can A* to the nearest known square (The one that renders the ‘best expected cost’) then best first across the unexplored area, or something like that.

But now I’m just rambling. :smiley:

For A*, you can cut a lot of corners if you can make assumptions about the map. From what you’ve said you can:

  1. Assume that the first path to a square is likely the best path to a square, which removes the need to ever revisit a tile. (If you need me to explain this, I can).
  2. Building on 1, if you can only move N,E,S,W then the Manhattan Heuristic is admissible and will always be the best path when you arrive at your goal (If you can move in diagonals, then the Euclidean Heuristic is better).
#18

I just dug up a pathfinding demo applet I made for testing my game’s A* implementation. It allows you to place obstacles, a start, and a goal, then watch the A* behavior as it searches for an optimal path:

http://www.potentialgames.com/cave/pathfinder/

#19

Thanks to both of you for your further insights.

Sproingie:
Taking a game like this into consideration, I daresay that even the most ineffecient pathfinding mechanism will still run acceptibly. Bear in mind that the game I’m making is slightly more traditionally Roguelike - so there are no ‘smooth’ transitions between tiles - just immediate movement onto the tile’s center point, then to the next and so on. This means that the impact of A* (even if horribly implemented) is unlikely to have much impact on how smooth the game feels, or indeed how CPU intensive it seems.

UprightPath:
I’ll always be using the Manhattan-style algorithm, since there’s only 4 directions (as you pointed out). This should mean at the very worst, any one node (barring the origin, of course) should have a maximum of 3 children, cutting down the intensive process involved in checking the diagonals. I know it’s all relative, but it should reduce unecessary overhead.

And you’re probably right - the first path is likely to be the best, unless I decide to start making horribly designed levels with twisting, turning long passages - but that’d be stupid in the context of this game which is supposed to be more focused towards events happening in rooms, rather than corridors.

This has definitely given me plenty of food for thought. Thanks again for your help and insights.

#20

For some odd reason, Firefox self-combusted upon trying to run the applet. Second time around it doesn’t seem to want to load. I was looking forward to seeing it!

I was planning on creating a similar tech-demo myself, in order to further enhance my grounding in the subject. You’ve pretty much summed up my intended goals in learning this facet of programming. Once I can nail this, that’s another string to the bow.