Perspective Transformation

Game Mechanics
#1

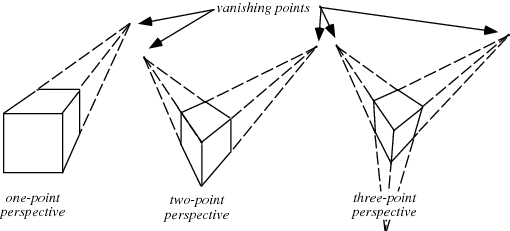
I want to tilt part of my game display like this:
http://www.jhlabs.com/ip/filters/PerspectiveFilter.html

After searching the web it looks like I need a PerspectiveTransformation:
http://download.oracle.com/docs/cd/E17802_01/products/products/java-media/jai/forDevelopers/jai-apidocs/javax/media/jai/PerspectiveTransform.html

However, its not clear to me if this is overkill or what I need to do this in real time, JAI sounds like its just for images, I want to be laying down more dynamic images. Any previous experience in this regard is appreciated.

J

#2

I asked something like this in the past: http://www.java-gaming.org/index.php/topic,20122.msg161495.html

#3

to obtain a per pixels correct perspective rendering (and not only a texture on a trapezoid) you may use this algorithm http://freespace.virgin.net/hugo.elias/graphics/x_persp.htm

it use recursion and no complexe matematical equations so it should be possible to make it run really fast.

also, as it recursivly render smaller parts, probably antialiasing the final image can be done on the fly

nb: if you always draw the same final trapezoid you can also simply precompute once a transformation array and use it several time

#4

Is it correct? I’d love to see a proof of correctness, because he seems to assume the linearity of a non-linear transform.

#5

strangly I think yes it is, for thoses cases : “Note, this only works for rectangles, not triangles. Actually it will work for any shapes that have at least two pairs or parallel edges”

I did not really verify but I beleave it work because the technic used is similar to the technic used when painting or making architecture draw (vanishing point).

also a fast test to verify texture center seems ok (and as it is recursive further centers should work too)

[attachment deleted by admin]

#6

I believed [1] when it said that the perspective transform doesn’t preserve straight lines, but I’ve worked through the algebra myself and concluded that it does. I’ve also done some looking around online and found how to compute a transform matrix directly[2]. Haven’t yet knocked up some JOGL code to do it, but I might get round to it.

Incidentally, and getting back on-topic, an approach I’ve used in the past[3] is to precompute the perspective transforms for each frame of an animation and store them in lookup tables so that for frame i, pixel (x,y) it tells you which subpixel in the “texture” (=untransformed image) to use.

[1] http://www.siggraph.org/education/materials/HyperGraph/viewing/view3d/perspect.htm
[2] http://alumni.media.mit.edu/~cwren/interpolator/
[3] See the page-turning animation of http://www.funorb.com/lexicominos/play.ws

#7

[2] looks very nice

[quote]A problem with a perspective transformation is that it does not preserve straight lines or planes, i.e., straight lines are not transformed into straight lines and planes are no longer planar after the transformation.
[/quote]
this is IMO false, but maybe more a problem (for me) of undertanding what he try to explain.

I mean, straight line appear as straight line once transformed by perspective, but if there is something regualry dispatched along the untransformed line it will appear not regulary dispatched on the transformed line (this is where the non linearity of perspective appear), also angle between line are not preserved

moving along a straight line (one pixels at once) on the tranformed image will usually produce a curve in the untransformed texture.

mapping give something like :
u = u0 + uaxScreen/z + ubyScreen/z
v = v0 + vaxScreen/z + vbyScreen/z

if we use a A=ua/z and B=ub/z it give
u = u0 + Ax + By (wich look linear, but as A & B are not constant and depend on z, it is not)

ok after re-reading my explanation is not that clear… but that the idea

#8

this is IMO false, but maybe more a problem (for me) of undertanding what he try to explain.
[/quote]
His perspective transform maps (x, y, z) to (x/z, y/z, z), which is non-linear. But that’s a very odd perspective transform. He should be mapping (x, y, z) to (x/z, y/z, 1). Then straight lines are preserved.