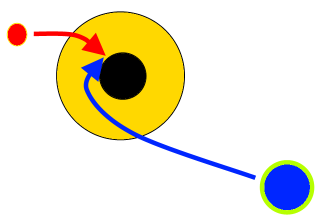
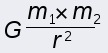Sounds like you’re wanting to simulate something like a gravity well, where an object is caught in the gravity field of a larger more massive object and is pulled inwards. Jonjava above does a good job of explaining the physics involved, i’d like to try and take it a tiny bit further.
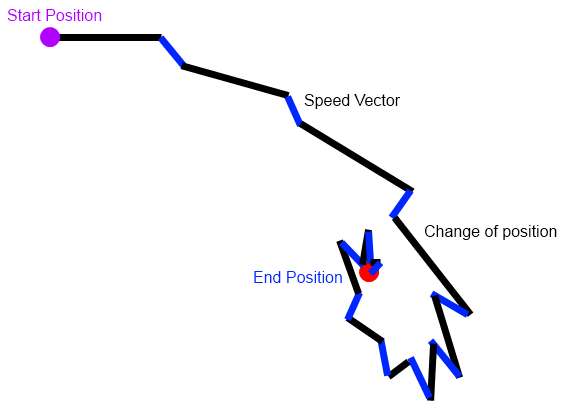
Once you calculate the force due to gravity on the smaller object, F, i think its useful to use this to calculate the acceleration on the object, since F = mass x acceleration, and work with acceleration instead of F alone. This way you can just use the acceleration value to update the velocity, then use the new velocity value to update the x and y position co-ordinates of the object.
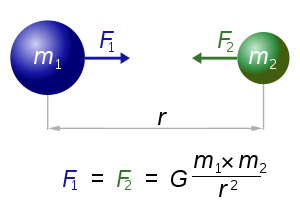
If you call m1 the mass of the larger more massive object, and m2 as the mass of the smaller orbiting object, then the acceleration of m2 is found by the following…
http://www.bahill.net/fma2.jpg
If m1 is much larger than m2, then the above shows that you can effectively drop the value of m2 from the calculation of acceleration due to gravity on m2.
Once you have the acceleration, you find it’s horizontal and vertical components. You’ve already nailed that in your code above using trig and the angle.
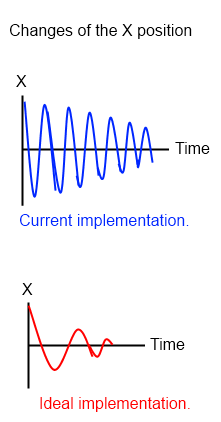
In each frame just keep adding the horizontal and vertical components of the acceleration to the horizontal and vertical components of the object’s velocity, and in turn add these velocity components to the x and y position co-ordinates of the object to simulate the effect of gravity, though rather roughly. A more accurate simulation would include higher order integration factors to accommodate the effects of a variable acceleration rate.
If you’re having bother splitting a vector into its horizontal and vertical components, check out the applet I knocked up to help visualise this at the link below. Click the mouse left button and drag it around the screen to see a vector and its horizontal and vertical components.
http://www.bahill.net/myApplet.html
Hope all that makes sense and is of some help to you,
cheers,
Bahill