A* Pathfinding, multiple paths with equal lengths.

Newbie & Debugging Questions
#1

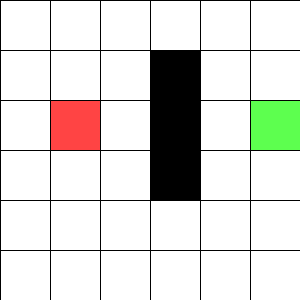
Hello, I have been working on A star pathfinding algoritham, and I’ve got it working for the most part but I was wondering if anyone could give me any advice as to what to do when I am faced with 2 or more paths that have the same movement cost, I was thinking of just picking one of the paths (that are of equal length) at random, but is there a quicker to do this?

I have included an image below, if the player was the red square and the goal was the green square, you can see there are two paths the player could take.

#2

It doesn’t matter. You’re worrying about things that don’t matter. If you actually already implemented the algorithm, you would notice that there are no 2 paths. Once you find shortest path, you return it.

How this works is you have 2 paths until the very end, and when you find a finishing tile, you only have 1 path. Just try it, you will only get 1 shortest path…

#3

Have a read of the very good introduction to A* of the Stanford University.

The problem of how to break ties is discussed on the second page.

#4

Ok, so in the below image what is stopping the red square from moving horizontally to the right until it hits the wall? Since the F costs of the squares will be the same up until that point.

#5

[quote]up until that point
[/quote]
Right, but that path doesn’t end at the destination, so it’s not even considered. Only a complete path (if one exists) will eventually be returned, that’s the point of pathfinding.

If you were to complete such a path by winding back around along the wall to the end point (the algorithm does this more or less btw), you will find it has a much longer length than the straight-down-and-around path, and is thrown out.