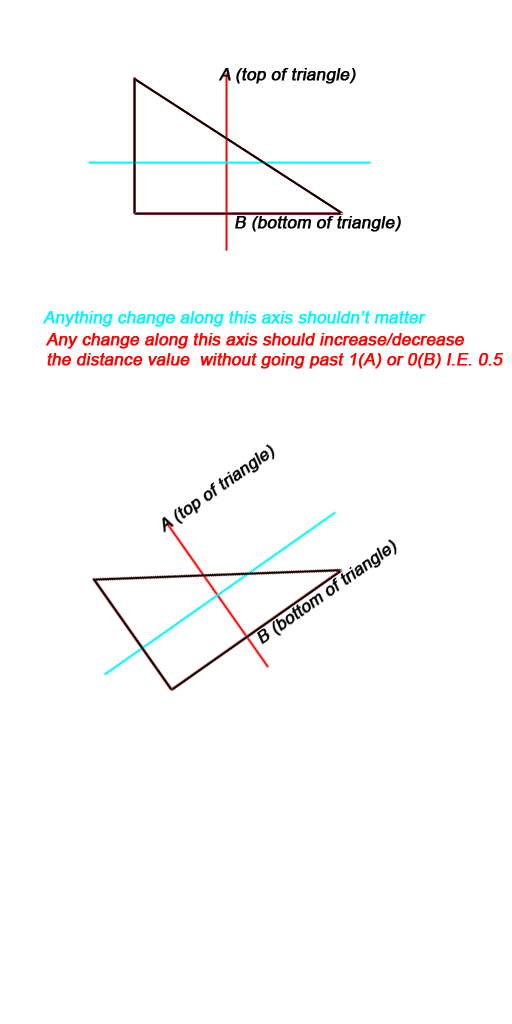
I made this for the lolz. Both methods appear to work just fine. Note the mouse position is slightly off because positions in the frame and panel don’t match exactly due to the menu at the top. Just look at where the cyan dot is.
import java.awt.*;
import javax.swing.*;
import java.awt.event.*;
public class TrianglePointContains extends JFrame implements MouseMotionListener
{
private static Vector3f mouseLocation;
private static Vector3f vertexA;
private static Vector3f vertexB;
private static Vector3f vertexC;
private static TrianglePanel sameSidePanel;
private static TrianglePanel barycentricPanel;
public TrianglePointContains()
{
super("Triangle Point Contains");
//totally arbitrary points
mouseLocation = new Vector3f(0,0,0);
vertexA = new Vector3f(200, 50, 0);
vertexB = new Vector3f(50, 350, 0);
vertexC = new Vector3f(350, 350, 0);
setLayout(new GridLayout(1,2));
sameSidePanel = new TrianglePanel( false );
barycentricPanel = new TrianglePanel( true );
sameSidePanel.setSize(400,400);
barycentricPanel.setSize(400,400);
add(sameSidePanel);
add(barycentricPanel);
addMouseMotionListener( this );
setSize(800,400);
setVisible(true);
}
public static void main(String[] args)
{
new TrianglePointContains();
}
public static boolean isPointInTriangle( boolean barycentric, Vector3f p, Vector3f a, Vector3f b, Vector3f c )
{
if ( barycentric )
{
Vector3f v0 = c.subtract(a);
Vector3f v1 = b.subtract(a);
Vector3f v2 = p.subtract(a);
float dot00 = v0.dot(v0);
float dot01 = v0.dot(v1);
float dot02 = v0.dot(v2);
float dot11 = v1.dot(v1);
float dot12 = v1.dot(v2);
float inverse = 1.0f / (dot00 * dot11 - dot01 * dot01);
float u = (dot11 * dot02 - dot01 * dot12) * inverse;
float v = (dot00 * dot12 - dot01 * dot02) * inverse;
return (u >= 0) && (v >= 0) && (u + v < 1);
}
return ( pointsAreOnSameSide(p, a, b, c) && pointsAreOnSameSide(p, b, a, c) && pointsAreOnSameSide(p, c, a, b) );
}
private static boolean pointsAreOnSameSide( Vector3f p1, Vector3f p2, Vector3f a, Vector3f b )
{
Vector3f diffba = b.subtract(a);
Vector3f diffp1a = p1.subtract(a);
Vector3f diffp2a = p2.subtract(a);
Vector3f cross1 = diffba.cross(diffp1a);
Vector3f cross2 = diffba.cross(diffp2a);
return ( cross1.dot( cross2 ) >= 0 );
}
private static Vector3f getAdjustedMousePosition( boolean barycentric )
{
if ( mouseLocation.x >= sameSidePanel.getWidth() )
{
return new Vector3f( mouseLocation.x - sameSidePanel.getWidth(), mouseLocation.y, mouseLocation.z );
}
return mouseLocation;
}
public void mouseMoved( MouseEvent e )
{
mouseLocation.x = e.getX();
mouseLocation.y = e.getY();
repaint();
}
public void mouseDragged( MouseEvent e )
{
mouseLocation.x = e.getX();
mouseLocation.y = e.getY();
repaint();
}
private class TrianglePanel extends JPanel
{
private boolean isBarycentric;
public TrianglePanel( boolean barycentric )
{
isBarycentric = barycentric;
}
public void paintComponent( Graphics g )
{
super.paintComponent(g);
Vector3f mousePos = getAdjustedMousePosition( isBarycentric );
boolean containsPoint = isPointInTriangle( isBarycentric, mousePos, vertexA, vertexB, vertexC );
Polygon p = new Polygon(new int[]{ (int)vertexA.x, (int)vertexB.x, (int)vertexC.x }, new int[] { (int)vertexA.y, (int)vertexB.y, (int)vertexC.y }, 3);
g.setColor( containsPoint ? Color.RED : Color.GREEN );
((Graphics2D)g).fill( p );
g.setColor(Color.BLACK);
((Graphics2D)g).draw( p );
g.setColor(Color.CYAN);
g.fillOval( (int)mousePos.x-2, (int)mousePos.y-2, 4, 4 );
}
}
private static class Vector3f
{
public float x, y, z;
public Vector3f( float setX, float setY, float setZ )
{
x = setX;
y = setY;
z = setZ;
}
public float dot( Vector3f other )
{
return x * other.x + y * other.y + z * other.z;
}
public Vector3f cross( Vector3f other )
{
return new Vector3f
(
(y * other.z) - (other.y * z),
(z * other.x) - (other.z * x),
(x * other.y) - (other.x * y)
);
}
public Vector3f subtract( Vector3f other )
{
return new Vector3f
(
x - other.x,
y - other.y,
z - other.z
);
}
}
}